\(\color{red}{\text{ Draft: Work in Progress..... }}\)
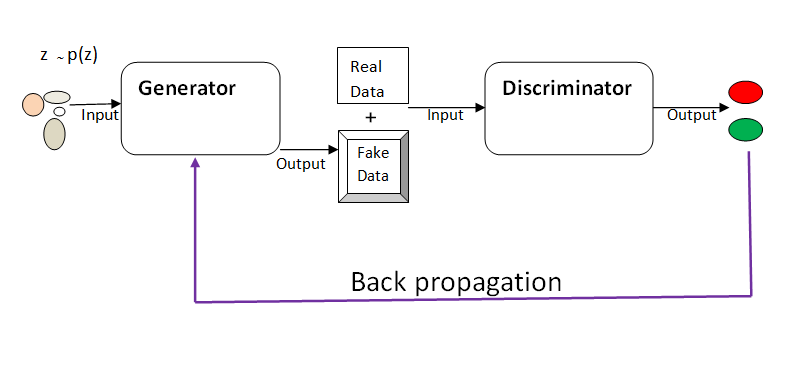
GAN consist of two competing models striving to outdo each other: the Generator and Discriminator models.
The Generator takes in random input and tries to generate real data (curves, images, texts, ).
The Discriminator is a binary classifier. It takes, as its input, the fake data generated by the Generator, and the real dataset and learn to tell whether the data is real or fake.
Through back propagation, the Generator updates its parameters using the output from the Discriminator.
The two models are trained simultaneously with the aim that the continuous competition will help produce data that is indistinguishable from the real data.
Diagramatically…
Given the objective function:
\[ \min_{G} \max_{D} F(G, D) = \log(D(x; \phi)) + \log(1- D( x^{'}; \phi)) \]
where:
$ z \sim p_{z}(z) $ is a random sample from distribution $ p_{z}(z) $
- $ x^{’} = G(z; ) $
$ x $ is the real data from distribution $ p_{d}(x) $
- Generator minimizes $ $ by maximazing log $ p(y= true|x^{’}) $
Discriminator maximizes by maximizing log \(p(y= fake|x^{'})\) and $ p(y= true|x) $
The models are trained simultaneously with the goal of obtaining a Nash equilibrium.